Chapter 85 — Blow-Ups
The Curve of Time, Chapter 85 —— Blow-Ups, in which Sienna returns to LA and seeks out Wassily.
Followed by a little deeper dig into mathematical blow-ups.
Listen to full episode :
— 85 —
Blow-Ups
Sienna returned to Santa Cruz and went for a run. She needed to clear her mind——process what she’d just learnt. It was scary to imagine that she had inadvertently caused chaos in a parallel timeline.
Down by the sand, a younger woman swept by her, running in the other direction. The younger woman, a teenager really, was in a world of her own. Headphones in place, she barely noticed Sienna——was certainly oblivious to her concerns. The woman could easily have been her younger self in another timeline, blazing past her older self, blissfully unaware of the turmoil that lay ahead.
How often did we brush by our future selves, without being aware? Maybe not with, literally, older versions of ourselves, but other people living through the trials and tribulations that loomed over the horizon.
Sienna’s mother had spoken to her about childbirth. It was a cliché; she’d called it life-changing. The idea was still an abstraction to Sienna, but at least she was aware of it as a potentiality. But, what of the other, smaller, still significant events that lay ahead? Events that would consume her world when she encountered them.
It was true that often you had to live something to understand that it was possible; that the possibility even existed. Even time travelers couldn’t see their own future.
Sienna stopped to stretch and watch the young runner disappear up along the shoreline, her feet leaving imprints in the sand that waves intermittently devoured. It was a weird thought that she existed in multiplicity, that maybe everyone did. All, without being aware that such was possible.
With no other particularly obvious path to follow, Sienna decided that to hell with it: she would look Wassily up. He, at least, was someone who had some connection to her past. And that Saskia had suggested doing so, suggested that she was implicitly giving Sienna permission. Not that she felt she needed her double’s permission; it was Saskia, after all, who had undone their pact, and sought her out!
∞
When she did look him up, she was impressed by what Wassily had made of himself. He’d clearly had a very successful post-doc and was now tenure track at one of the best universities in the country. She skimmed through a few preprints she found on his rudimentary department webpage. His, was a world of beautiful geometry.
Sienna made a faster return to LA than her trip north, and in the UCLA math department she consulted the directory board of faculty headshots. Wassily’s office was on the sixth floor. His door was open and she saw him before he noticed her. He was at his desk, pencil in hand, sketching. Between flurries of visual brainstorming, he’d idly tap his lead tip on the paper near the periphery of his doodles. Sienna knocked on the doorframe.
Wassily glanced up from his work, but seemed not entirely surprised to see her. “Saskia. What brings you here?”
For a split second, Sienna considered running with Wassily’s use of her first name. She enjoyed the comfort it gave her, especially coming from his mouth. But, in admitting that enjoyment to herself, perhaps she also had to admit that some things do change. For one thing, the Wassily in front of her even looked like a young professor. “Actually, it’s Sienna now.”
“I always loved your middle name.” Wassily took Sienna’s change of name in stride, or perhaps he was just more interested in another question: “Did you try using your second superpower?”
Sienna cocked her head, and squinted at him. “My second superpower?”
Wassily nodded slowly. “Your super strength.” He’d caught Sienna in an unexpected mental blank, or . . . “You really aren’t Saskia, are you?”
Sienna shrugged and raised her hands, palms up.
“So there really are more than one of you floating about.”
Sienna’s face confirmed his guess.
“But you’ve seen Saskia?”
Sienna admitted that she had, both back when everything started. And then again, a few days ago.
“Have you felt it? Yourself splitting in two?”
“Me?”
“Saskia never noticed when it happened.”
“No.” Sienna indicated a paper Möbius strip that was collecting dust in a small gap on Wassily’s shelf, a shelf that was otherwise lined with yellow-spined books. “I imagined that maybe time was like a Möbius strip: when you loop back you just come back on the other side. It didn’t really make sense.”
There was a sudden twinkle in Wassily’s eyes. “Maybe . . . Forget macro structures, though. There should be a problem every time you turn time about. The singularity of reversing time.”
Sienna nodded. “Sure, the problem of why I don’t bump into my earlier self.”
“But mathematicians have a way of resolving that problem. It’s called a blow-up.” Wassily could see that, at best, Sienna vaguely recalled what he was talking about. He crossed to his whiteboard, picked up a scrap of felt that lay crushed on the pen tray among a rainbow of markers. With easy indifference, he cleared the center of the board, erasing multicolored loose gestural strokes that depicted pretzel-like shapes connected with arrows and symbols, alpha numeric, Roman and Greek.
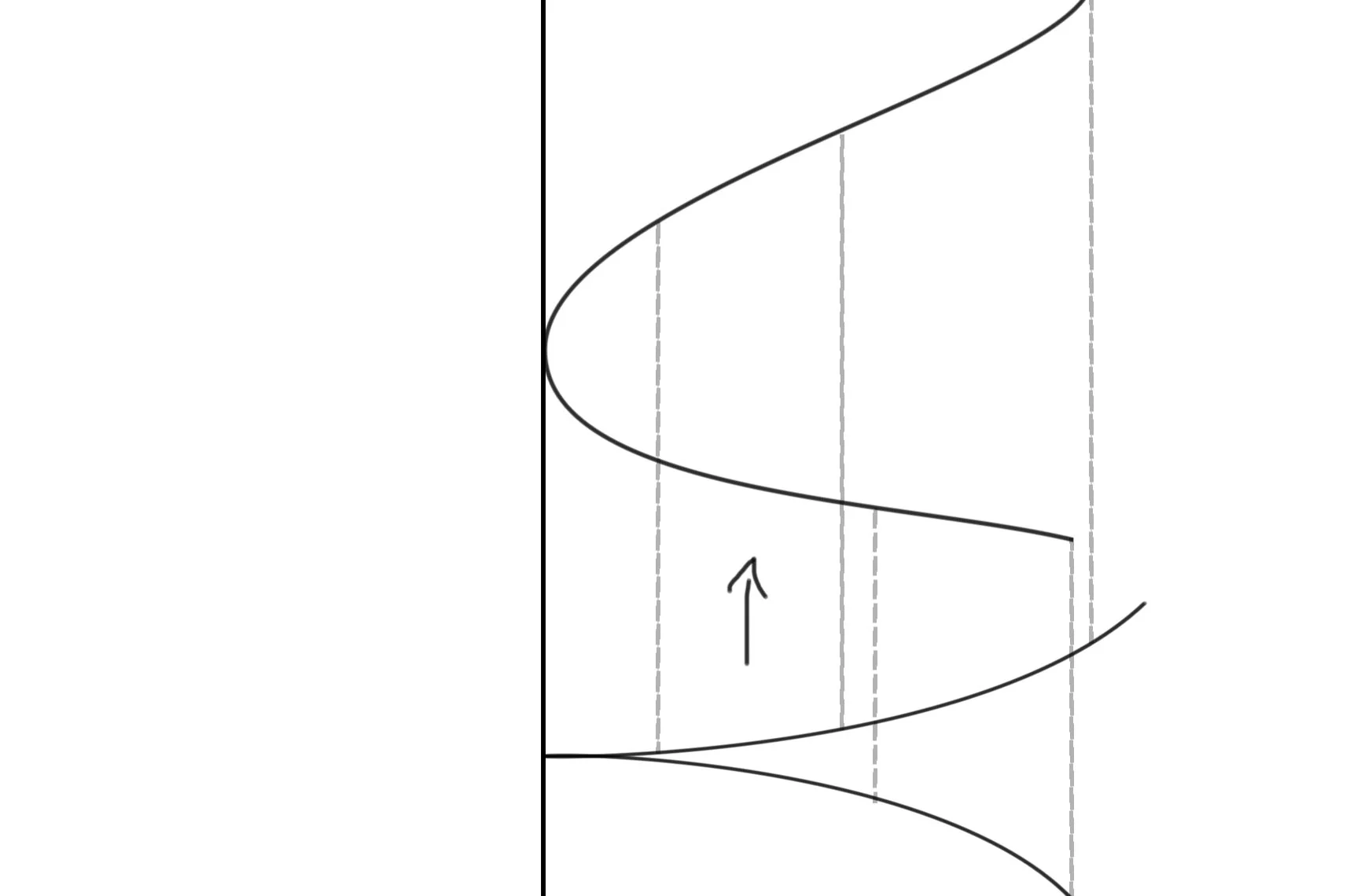
In the white space he’d liberated, Wassily started sketching. “Start, by imagining a whole lot of straight lines intersecting, and see how those lines get separated when we keep track of direction using the vertical dimension.” Wassily stood back to admire his picture:
Sienna nodded.
“That’s called a blow-up, and it resolves the singularity at the crossing point. Now, if you think of a point on a curve in the 2D plane as a point, plus a direction, then you could take each point and graph them in 3D; every point on the curve corresponds to the point’s x, y pair plus a direction, the z height. If you do that, and you come into a cusp point, you could imagine that you’re actually coming in with a very slightly negative slope and leaving with a very slightly positive slope and the only point you have zero slope is at the cusp point. Then, in 3D, the curve no longer overlaps as it comes in and goes out of the cusp point. But you only keep track of the extra dimension at the cusp point.”
Wassily wiped his board clean and drew a second picture:
“You think there’s some sort of invisible dimension that I’m turning around in when I stop and reverse time?”
“Yes!”
Sienna squinted her eyes shut, trying to visualize it.
“The blow up kind of takes you to another nearly identical copy of the world. Think of them as planes”——Wassily used his hands to indicate flat planes parallel, one above another——“and it is in the plane above your own that you encounter copies of yourself.”
Sienna pinched the bridge of her nose, travel fatigue was catching up with her.
“Where are you staying?” he asked.
She shrugged. “I haven’t got that far yet.”
“You want to get some air?”
∞
Wassily took Sienna to the Mathias Botanical Gardens, on the hilly east side of campus. It felt almost as if he’d transported her back up north, only there was a diversity of trees——from Eucalyptus, to palms——to complement the redwoods. There was even a rocky creek that ran through the gully in which it was situated.
As they strolled along the winding paths, Sienna wrestled with the implications of Wassily’s theory. “So resolving the singularity solves crashing back into myself, but what does that have to do with forking off a new time-line?”
“Maybe rather than forking your world, there were always two distinct timelines. They looked identical up to a point . . . but what you think of as forking, is not so much that you change your timeline; but that you slip over and enter a new one.”
“Whoa.” Sienna wiped her forehead with the palm of her hand.
“The parallel timelines are identical to the point that you switch over——you wouldn’t even know another future was possible, but that you’d lived it and gone back to the switchover point.”
“But I can only ever see three of the dimensions, and, kind of feel the fourth?”
“Exactly. You can’t see time, so what’s to say there aren’t other dimensions that you’re blind to. You’re a Flatlander in hyperspace. It’s no wonder you can’t pick and choose which timeline you jump into.”
Sienna stopped to marvel at a burnt orange flower that reminded her of the salamander’s underbelly. She looked back at Wassily. “So how do we test whether your theory describes the reality we’re living in?”
Wassily just laughed. “I’m a mathematician. I’m just happy to come up with a model to explain what we’ve seen. Scientists are the ones that use theories for predictions.”
This was what she liked about him, his unapologetic passion for the mathematics.
He smiled a crooked smile. “My model doesn’t exactly have predictive power.”
Sienna gazed up into the canopy of the giant trees that surrounded them. Within the same timeline, she could still get confused about where she was.
“For me,” Wassily started, “for me, it’s enough to think that the universe might be stitched together in a wonderfully multidimensional fabric. I like that better than a model that’s bifurcating left and right.”
That was chapter 85, Friends, I hope you enjoyed it!
Obviously, there were some sophisticated mathematical ideas in today’s chapter, and in the interest of keeping the story moving I didn’t want to bog us down. But given that this is the commentary section, I thought I might highlight one subtlety that the astute among you might have noticed.
To recap, the idea of a mathematical blow-up is to not only keep track of the x,y coordinates of the curve in two space, but append to those coordinates a direction coordinate, at least and near our cusp point. Thus, when coming into and heading out of a cusp point, since your curve is moving in opposite directions it won’t be represented by the same point; kind of like, just at that point, there is a momentary extra dimension. Again, as Wassily said, you can kind of forget about the direction coordinate until you arrive at the cusp point and then, when you do, imagine that you’re keeping track of your pirouette, thus keeping the same x,y coordinates, but noticing that your z coordinate shifts when you leave the cusp point above where you came in. Neat idea right?!
Anyway, here’s one subtlety that Wassily glossed over that some of you might have noticed: if you’re thinking about the slope at that point, then the slope going in and out might well be just the same, just that you’re traveling in the opposite direction (and, no, that doesn’t mean you’re traveling the negative of the slope you entered with——the negative of a given slope would just mean heading down in the 2D rendering, instead of heading up).
So, how do mathematicians make sense of this?
Well, in the case of the cusp point above, you can imagine that the slope at the cusp point is zero (ie. the curve is flat), and it comes in slightly negative from below and heads out slightly positive as we come out of the cusp. Thus the “resolved” curve——aka the blow-up——is a curve that we’re seeing in three dimensions that sits directly above the original cuspidal curve that sits in the two-dimensional xy-plane. My buddy, Rob, made a delightful rendition of this blow-up on the magical mathematical website Desmos. I highly recommend having a look. You can use your cursor to drag the whole picture around and get a good look at it from different perspectives.
One last fun extra piece: if we stretch that blow-up line segment out to take up a whole dimension (in this case think of slope going from minus infinity to infinity) then every direction corresponds to one point on the line and the vertical direction corresponds to what mathematicians would call “the point at infinity” which is where the line has both infinitely positive and infinitely negative slope. This is kind of the jumping off point for what mathematicians call projective space. It’s all very related to the idea behind why train tracks look like they’ll meet if you were somehow to follow them all the way to the horizon.
Anyway, enough digressing. I suspect I’m at risk of having muddied the waters, more than cleared them out. One last note, today’s was the only chapter that has explicitly referenced Edwin Abbot Abbot’s Flatland. Hope you caught the acknowledgement!
Until next week, be kind to someone and keep an eye out for the ripples of joy you’ve seeded.
Cheerio
Rufus
PS. If you think of someone who might enjoy joining us on this experiment, please forward them this email. And if you are one of those someone’s and you’d like to read more